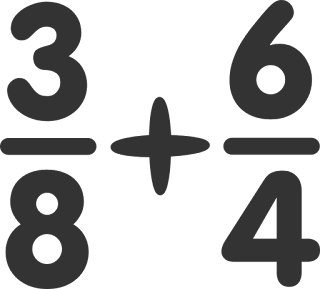Chapters found in Algebra 1

Algebra 1 is a second math course found in the high school and it can guide the person through many other expressions with the system of equations, real numbers, function, exponents, inequalities, rational and radical expression and polynomials.

The algebra math had been divided into 12 chapters and each one of these chapters had been divided into many lessons.    

This topic is the overview of the fundamental ideas with the tools available in the algebra

 It teaches

-         Solving the equation by learning solving the linear equation which has just one single variable

-         Solving of inequalities: learning about solving the inequalities using  just one single variable

-         Working with the units: this is a unit that teaches about the general concern  of modelling concern before diving in the modelling situation with many types of equation and function under algebra curriculum

-         Linear equation with graphs: you can learn about the linear equation which contains two different variables and how such can be represented in the graphical lines with value tables

-         Functions are the mathematical entities which assign the unique output in order to give the inputs. This is a topic meant to evaluate, to graph and to analyze while creating different functions types

-         Linear word problem: it is easy to solve such word problem which involves the real world which may be represented in the linear functions and equations

-         Sequences: you can learn different ways for which you may define the sequence by using or constructing the arithmetic with geometric sequences.

-         Equation system: learn the way of interpreting the solution system of the linear equations and to solve them.

-         Inequalities (graphs and system): within this system, the user will study the inequalities and then graph each one of them. This will help to get the solution and it helps to explore inequalities system with multiple inequalities at once and to use them in order to describe the situation in the real world.

-         Absolute value with piecewise function: in this chapter, the person will learn the way of graphing the absolute value function.

-         Rational exponents with the radical: in this chapter, you learn the expression of the rational exponent, the radical expression and the relationship which exist between the two forms of such representation

-         Exponential growth with decay:  you will learn the way that you may interpret basic exponential function and to construct, analyze or make up the graph.

-         Polynomials: you may learn how to subtract and to add polynomial  expression

-         Factorization: this helps to learn writing the polynomial expression with the product of the linear factors

-         Quadratics: this the system that teaches how  to analyze and to graph the quadratic functions

-         Irrational numbers: you can learn on the irrational numbers so that you can identify them easily.

What are algebraic equations? Learn how to solve them

Algebraic equation is also known as polynomial equations. A polynomial expression is made up of constants and variable, combined using mathematical operators. When a polynomial expression is equated to some constant value, it becomes polynomial equation. To understand this in simple terms, go through the following example.

x²-5x+6

Is a polynomial equation, here x is a variable, 5 and 6 are constant and mathematical operators used are addition and square, but

x²-5x+6=0 is a polynomial equation or algebraic equation because it is equated to a constant (in this case zero).

The general form of a polynomial equation is

As one can notice the power f x keep on decreasing. The above equation is called a polynomial degree of order n.

What is degree of polynomial?

Degree of a polynomial is the highest power of variable. Degree of a polynomial is always a non-negative integer.

Depending upon the degree of polynomial, polynomial may de defined as quadratic equation, Linear equation or constants.

To be very particular a polynomial equation of degree 2 is called quadratic equation, polynomial equation of degree 1 is called linear equation and polynomial equation with degree of polynomial zero are nothing but constants values.

In this module we will focus on quadratic equations

The general form of a polynomial equation is ax²+bx+c= 0

Here,

·         a is the coefficient of x²

·         b is the coefficient of x And

·         c is the constant term

To solve quadratic equations there are three methods available, they are:

·         factorization

·         completing the square method

·         using quadratic formula

Let us see each method is detail.

Factorization method

In this method the quadratic equation is decomposed into 2 factors. (What are factors? Factors are those values, which if substituted into the original equation, then it result out to zero. ) for example in our example, x²-5x+6 =0 the equation can be written in the form, (x-2) (x-3)=0 . If one opens the bracket and multiply the terms then we get the original equation x²-5x+6 . Therefore (x-2) (x-3) are known as factors of the equation x²-5x+6 =0

How to find factors of any quadratic equation?

To find the factors of any quadratic equation, follow these steps:

Step 1 Decompose the middle term, i.e., the terms containing the x and it coefficient into 2 parts, such that the product of those two terms should be equivalent to the product of x² term and the constant term. Also, the summation of those decomposed two terms should give back the original middle term.

Step 2 Take common out from the first two terms, and from second two terms in such a way, that you get common factor among both these terms.

Step 3 Again take the common factor out, and then you are left with 2 final factors of the original equation.

If the above mentioned steps are not clear to you, go through the following steps:

Let’s start with

x²-5x+6 = 0

Now let us write 5x as -2x -3x

x²-2x -3x+6 =0

This is so because, product of (-2x) and (-3x) is (+6x²), which is same as product of (x²) and (6), i.e., (6x²), the product of x² term and constant term.

Now, take x common out from x² and (-2x) and (-3) common out from (-3x) and (6)

The equation becomes x(x-2)-3(x-2)=0

Now take (x-2) common out

 (x-2) (x-3)= 0

These are the factors of the original equation x²-5x+6=0
 

The values of x in this case would be 2 and 3.

Know features and benefits of algebraic software

Have you ever wondered how algebraic software could teach you how to effectively solve the algebraic or polynomial equations? If not so then here you will find everything related to the amazing mathematics software. Many students seek the help of coaching or tuition classes so that they too can effectively solve the problems very faster and quickly. But they remain in doubts as they lack some of the basic of the topics. Now this problem can be solved with the help of software that let the students build their concepts and capture useful formulas. So, go through the article and read everything about it.

There is much software available online that can be downloaded very easily on the computer, and the student can solve the problem no matter what may be the origin of the problem. Because of the excellent programming and cost-free feature, millions of the students have already exploited the benefits of it. You can solve algebraic equations, matrices, graphs and also the geometry problems very fast and correctly. The student will able to grab the basic of the topics that will help them in the future exams. You will also get the best and positive results if you make use of the mathematics software.

Some of the features of the software:

·         The software makes use of the interactive learning methods that the tuition or the coaching classes may lack. This makes the learning program more effective and easier for the students.

·         The dynamic and the appealing lessons make use of wonderful graphics and animations that add extra value to the learning programs.

·         The student can learn the formula used in elementary algebra, and they can expand their thinking skill with the help of it. The students will master problems and concepts in a short span of time. This also helps to increases the level of confidence that is really very important to tackle all type of problems.

·         It has made a breakthrough in the field of understanding and applying concepts to solve the problems very quickly. It acts as personalized coaching that helps the students to learn concepts through visual means and methods.

·         The software let the student seek the self-studying lessons while they were seeking other curriculum activities. They are known to be an adaptive instructional software as anyone can be benefited with the help of it.

Benefits of the software:

·         The software helps the student to achieve educational excellence, and they are filled with most of the concepts with a clear vision.

·         The student can design their own problems and equations so as to get practiced with most of the numerical. This will let them solve the problem easily in the exams with any problem or distraction.

·         The supplement provided in the software help the student to create plans for the study. So, this will increase the flexibility of the students greatly.

·         The demonstrations in the programs will expand and boost their math skills and they too can effectively solve the problems with the dynamic course.

This is all about the algebraic software that let the students solve the expressions very easily. 

How to change Decimal into Fraction

Math is not something easy for most people. There are some concepts that are difficult, and one of them is that you can change the fraction to the decimal and it may be confusing according to the fraction.   Even if you are using the calculator or do this on your own, there are different methods that you may follow if you want to turn the fraction into decimals.  

Know the available terms: every number in the fraction comes with its own names. A top number in the fraction is known as the numerator, and the bottom number is known as the denominator. The fraction does express the idea of a numerator, and it is divided by a denominator.  The example is three over four which is 3/4, and this means that it is 3 that should be divided by a 4. You may use the idea in changing fraction in decimals.    

Rewrite the fraction: you should start by changing the decimal in the fraction and to rewrite the fraction as the workable math problem. 

  

Solve the problem:  you should start by solving x if it is found in the problem before you can change the fraction in the decimal.  If the fraction is a number of itself, then the answer is going to be 1.  

Solving the fraction using remainders; you can find simple fraction which has the remainders and then divides them.  When there is a remainder, then you should add zero after the decimal.

-        Whenever it is possible, you have to solve the division problems and make sure that there is no remainder.  

-       Keep track of the place where the decimal has to be.  You may get wrong decimal since you may have removed the place where the decimal point has to be.

Solving fraction that has repeating decimal; sometimes the fraction cannot be divided well into other numbers.  If this takes place, you will have the repeating decimal.  This will lead to the remainder, and the decimal number will continue to repeat itself.

-       When the remainder is the same, even if you continue to add zero, the same remainder will be the same, and the same number you are getting will continue to come

-       In writing the answer, you should cut off decimals at the amount of the places which are needed for the assignment. You may put the straight line over the number that repeats itself to show that it is the same that comes back.

Changing of the complicated fraction; you can find some fractions that are more complicated compared to others since it takes more time in dividing them. You should use the remainder until it gets finished.

Solving the irregular fraction; the complicated fraction has a definite decimal answer. You can find some fractions that have always the remainder. Contrary to repeating decimal, the decimal will not have pattern.  Even if you may continue, you will still have the remainder so you should write only the decimal up to the required number.

Where to get Algebra Help

If you want algebra help, you can get it from worksheets, calculators, and lesson that have been developed to assist the students or teachers while learning or teaching algebra. 

Lessons: you can explore the lessons available on algebra such as simplifying, equation or factoring among others.

Calculators: you can use calculators if you are having problems in solving some equation. The calculator can show the best answer with the step by step solution on how you may solve the same equation.  With these calculators, the students had been able to solve over 15 million equations. However, the calculators are not meant to solve the equation only since they can help you to know step by step method that you can use while solving the problem at hand.

Worksheet: If you need practice with some new problems, then you can use the worksheet section. You may compare the answers against the answer keys, and then you may see step by step solution for every problem.

If you still need to get extra help, you can contact a math tutor or an algebra tutor online, and he will be ready to help you to out.

Most of the students do not like the idea of having to learn algebra while in high school and in college since they do not think that they may use it in their everyday life.  However, learning algebra helps in solving financial problems, business solution, and even everyday dilemmas. If you want to succeed with algebra, you have to start by understanding the situations that require formulas with concepts. The best part is that the common life problems require highly recognizable technique and they are widely applicable. You can use the quadratic equation if you want to find the minimum or the maximum of a certain value. You can then use the linear equation if you want to determine which type of the service you are able to afford if the service does involve the flat fee and the rate. Use two linear equations in the system if you wish to compare two different plans and you want to figure out the turning point that makes a plan to be better compared to another.

You can use exponential equation if you want to represent or to solve the saving on the loan situation. If you are not able to know which type of the equation involved, you may attack the situation using real-life situation and convert the idea into numbers. If you are writing the equation starting from your words, you should not copy down each part of problem or orders. You should consider numbers and the unknowns and how they can relate from one to another. The values may be expected to be smaller or larger. You may use common sense if you are writing out an equation. If you are not sure, you can draw a graph or a picture. This can help in brainstorming how to use the equation which may fit better the situation.

Benefits of Understanding Mixed Fraction Calculator

Like the saying, education is the key to success, and most people benefit from training. It is the right of the children to be educated. Most of the government has set the rules that ensure that most children can attend schools. There are severe consequences to the parent who do not introduce their kids to education. Mathematics, statistics, qualitative analysis, and sciences involve mixed fraction calculator. Most students who understand the combined fraction calculator can easily solve other mathematics challenges. It is essential to make sure that you pay attention to the teaching staffs during these lessons. The following are the benefits of studying and understanding the mixed fraction calculator.

fraction calculator

Increase you mean grade

Mixed fraction calculation is one of the major topics that are in mathematics. Understanding the topic can make sure that you handle most of the units in mathematics and statistics. Following the unit can ensure that you pass mathematics and other subjects. These can result to increase of your total mean grades in school. The increase of the mean grade leads to recognition of your performance by the school fraternity. These can make sure that you have a great time in school time. Most of the student can like spending a lot of their time with you to be able to learn from your skills.

Increased reward

Rewarding the best students in the school motivates the rest of the school to work hard. The rewarded students are also motivated to make sure that they can increase their final grades in the school. Most of the educational institutions have the special day where they reward the best student in most subject and units. Being the best in the mixed fraction calculations can make you the best students in most subjects and units. These can make sure that you receive most gifts and rewards from the school. The parents and guardians enjoy seeing their kids performing well in their academic works.

Simplifies life

Again, most people have to manage big empires and business when they are adults. It can be straightforward when they can handle most of the calculation in the business. Ability to handle the mixed fraction in the school can assure that your future can be great. You don’t need to hire most employees to help you with the calculation in your company. These can make sure that your empire can develop with no time.

Encourage asking questions

Mathematics has challenges that at times it is difficult to ask for explanations. Doing the mixed fraction can make sure that you discover the areas that you have problems. It can be easy to approach a teacher when you know the specific areas where you need assistance. Again a simple explanation can make sure that you can understand the whole content. Most of the students can also approach you when they need your help in most of the subjects. The teachers can use you to explain most of the cases to other student or teach others. Most of the students fear the teachers thus they can understand well when their students take the opportunity to explain to them. 

How to Simplify Radicals

If you want to learn how to simplify radicals, you should know how you can convert the expression with the rational exponents, how to convert expression using rational exponents to the radical equivalent, using of the exponents law in order to simplify the expression with the rational exponents  or using rational exponents in order to simply radical expression.

Most of the time, the square root has to be written by using a radical sign. However, it can also be represented by using its root. You may use the rational exponents and not the radical. The rational exponent is the exponent used as a fraction. The example is instead of writing the root of 4, it will be written 4^1/2.

You may have to get used to raising the rational exponents; however, the rational exponents may help in simplifying the problem.  You should be aware of which relationship found between radicals, exponents and fractional.

Fractional and radical exponents are the alternative way that someone can use to express something.  You may have seen how square roots may be expressed as exponents at the power of just one half.

When it is cube roots, then the cubing of the number, it will raise the power up to three.   The exponent is used to refer to the quantity which is found at the left if the grouping of the symbol was used.  Like you may write the expression using the rational exponent with the radical expression, it is possible to express the radical expression by the use of the rational exponents.

The rational exponents using a numerator which is different to one: All the numerators for the fractional exponents, a person may use the fractional exponents which have the numerator which is not 1 in order to express the roots.

In order to write the radical by the use of the fractional exponents, power at which the radical had been raised, it will become the numerator, and the root will become the denominator.

The rational exponents have been subjected to same rules as it happens with other exponents and they do appear in their algebraic expression.  The simplification method can give different results according to which context of a problem.  It will be easier in using one method and not the other.  It is possible to simplify the expression faster by the use of the rational exponents compared to the pull out method.

Another alternative method is working on simplifying the radical using the factoring.   For a complicated expression of two variables, the racial and the fraction, it is good to know the steps to use when it comes to fractional exponents, and it may help the user to simplify it more.  Depending on the type of questions, the user will use negative exponents, fractional exponents and the rule of the exponents so that they may simplify the entire expression.

Rewriting radicals by using fractional exponents, it may be useful in simplifying the radical expression.  While working with the fractional exponents, you should remember that fractional exponents are subjected to the same rules like other exponents if they appear in the Algebraic expression.